티스토리 뷰
트라이(Trie)
- 문자열에 대한 검색을 빠르게 도와주는 자료구조
Abstract
- 문자열에 대해 이진탐색트리를 적용하면 ➡️ 문자열의 길이(M) + 문자열의 총 개수(O(log(N)) ➡️ O(Mlog(N)) 의 시간복잡도
- 트라이를 적용하면 ➡️ O(M) 으로 문자열 검색이 가능
e.g.) [bear, bell, bid, bull, buy, sell, stack, stop] (N = 8)
BST for Strings

- 문자열의 개수(N)만큼 비교하기 때문에 O(logN)
- 가장 길이가 긴 문자열의 길이가 M이라면 두 문자열을 비교하는데 O(M)
- 총 O(MlogN)의 시간복잡도
Trie for Strings
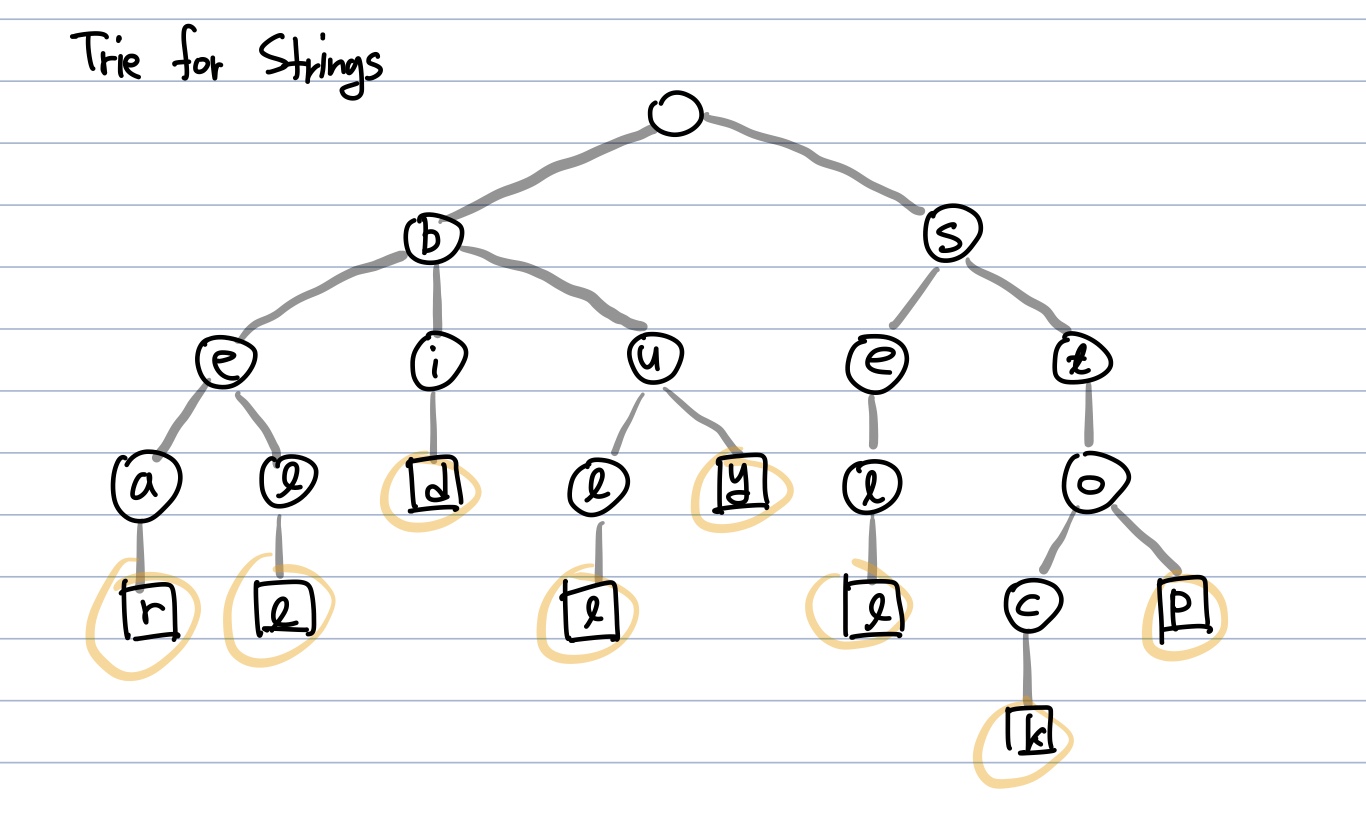
- 트라이(Trie)를 활용 한 Tree의 leaf node의 갯수는 문자열의 총 개수(N)과 동일하다
- O(M)의 시간복잡도 (가장 길이가 긴 Strings의 길이(M)만큼만 탐색하면 된다)
특징
- 문자열을 단순하게 하나씩 비교할때보다 훨씬 효율적
- 각 노드는 자식에 대한 포인터를 모두 저장하므로 공간을 많이 차지
- O(포인터 크기 * 포인터 개수 * 총 노드의 개수)만큼의 공간을 차지한다.
적합할 때
- 검색어 자동완성, 사전에서 단어 찾기, 문자열 검사
- 각 노드에 저장할 필요 없이 문자열의 접두사를 얻을 수 있다.(지나온 경로가 곧 그 문자열의 접두사들)
참고한곳
'자료구조' 카테고리의 다른 글
| B+ 트리(B+ Tree) (0) | 2021.12.24 |
|---|---|
| B 트리(B-Tree) (0) | 2021.12.24 |
| 해시(Hash) (0) | 2021.12.23 |
| 이진탐색트리(Binary Search Tree, BST) (0) | 2021.12.23 |
| 트리(Tree) (0) | 2021.12.23 |
Comments



