세그먼트 트리(Segment Tree)

세그먼트 트리(Segment Tree)

• 여러개의 데이터가 연속적으로 존재할 때 특정한 범위에 속하는 데이터들의 합을 구하는 방법

---

방법 1️⃣ 단순 배열을 이용해 선형적으로 구하기
e.g.) [5 8 7 3 2 5 1 8 9 7 3]

• 데이터를 순차적으로 하나씩 더하므로 O(n)의 시간복잡도

index	0	1	2	3	4	5	6	7	8	9	10	11
array	5	8	7	3	2	5	1	8	9	8	7	3

➡ array[1]부터 array[10]까지의 부분합 : 58 (차례대로 하나씩 더함)

---

방법 2️⃣ 트리 구조를 이용하여 구하기

• 각 노드마다 구간합을 저장하여, 트리의 특성상 O(logN)의 시간복잡도

 

구간합 트리 생성

 

---

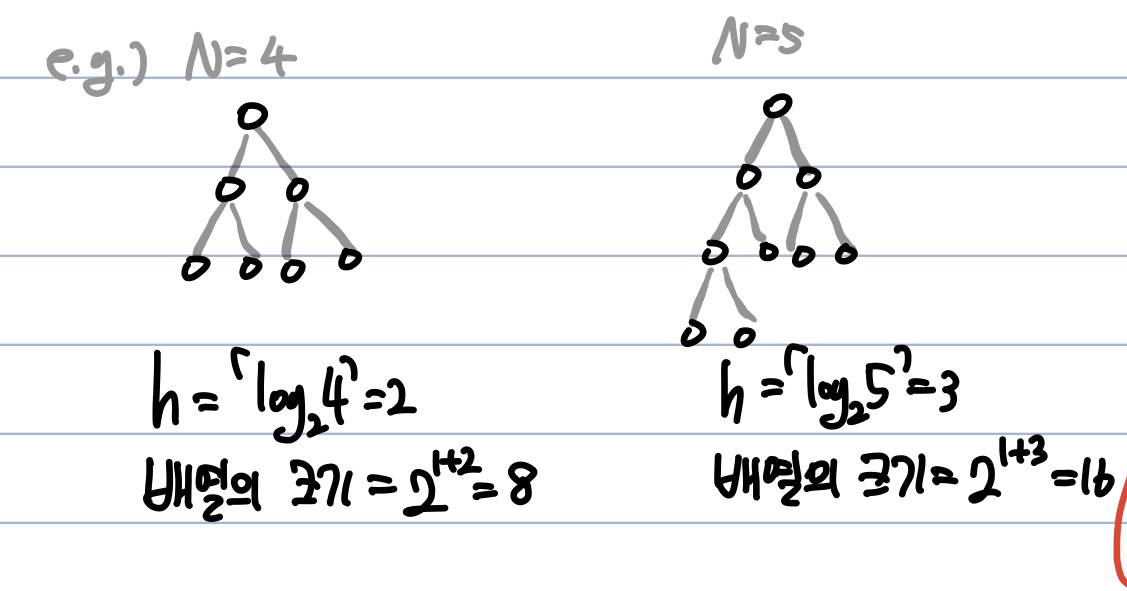
트리 배열의 크기

• 기존 배열의 크기 => N = Segment Tree에서 leaf node의 개수
• Leaf node가 N개면 트리의 깊이는 H => ceil(logN)
• 배열의 크기 => 2^(h+1) (트리 노드의 개수는 a0 = 1, a1 =2, 공비 r = 2인 등비수열, 따라서 1+2+4+...+2^h = 1 + (2 * 2^h -1 ) / (2 - 1) = 2^h+1)

포화이진트리일때 깊이가 3이면 총 15개의 노드가 존재한다. 남는 (2^(3+1) = 16) 1개는 사용하지 않는 0번 index

 

---

연산

• 구간합 탐색

int sum(int index, int start, int end, int left, int right){
  // 구간합을 구할 범위 : left, right / 노드의 시작과 끝 index : start, end

  // 구간합을 구할 범위가 현재 노드의 범위 밖에 있는 경우
  if(left > end || right < start) {
    return 0; // 무시
  }

  // 구간합을 구할 범위 안에 현재 노드의 범위가 속하는 경우
  if(left <= start && right >= end) {
    return tree[node]; // 현재 부분합을 그대로 반환
  }

  // 구간합을 구할 범위가 현재 노드의 범위와 일부 겹치는 경우
  // 혹은 구간합을 구할 범위가 현재 노드 범위 안에 있는 경우
  else {
    int mid = (left + right)/2;
    return sum(index*2, start, mid, left, right) + sum(index*2 + 1, mid+1, end, left, right);
  }
}

• 구간합 수정

 

void update(int start, int end, int node, int index, int diff){
  // start, end : 현재 범위의 시작과 끝 인덱스
  // index : 구간합을 수정하고자 하는 배열의 인덱스
  // node : 현재 노드 번호
  // diff : 수정할 값 

  // 수정할 노드의 인덱스가 현재 범위 밖에 있는 경우
  if(index < start || index > end) return; // 무시

  // 수정할 노드의 인덱스가 현재 범위에 속하는 경우
  tree[node] += diff; // 누적합 값 수정
  int mid = (left + right) / 2
  update(start, mid, node * 2, index, diff);
  update(mid + 1, end, node * 2 + 1, index, diff);
}

 

=> 탐색/수정에 대해 각 노드가 구간합을 가지고 있으므로 O(logN) 의 시간복잡도

 

 

 

---

참고한 곳

• https://ssungkang.tistory.com/entry/Algorithm-%EC%84%B8%EA%B7%B8%EB%A8%BC%ED%8A%B8-%ED%8A%B8%EB%A6%ACSegment-Tree
• https://blog.naver.com/ndb796/221282210534