티스토리 뷰
반응형
Red-Black 트리(Red-Black Tree)
Abstract
- 불균등상태를 방지하기 위해 균형을 맞추는 이진탐색트리 의 일종
- 레드블랙트리의 Search는 O(logN)
조건
- Root Property: 루트 노드의 색깔은 검정(Black) 이다.
- External Property : 모든 External Node(자식이 없는 노드)의 색깔은 검정(Black) 이다.
- Internal Property : 빨강(Red) 노드의 자식은 검정(Black) 이다. (= No Double Red, 빨강 노드는 연속해서 나올 수 없다.)
- Depth Property : 모든 leaf 노드에서 Black Depth는 같다
- 모든 leaf 노드에서 root 노드까지 가는 경로에서 만나는 검정(Black)색 노드의 개수는 같다.
Restructuring & Recoloring
- Double Red를 해결하는 2가지 전략
e.g.) 삽입하는 Node의 색은 항상 Red
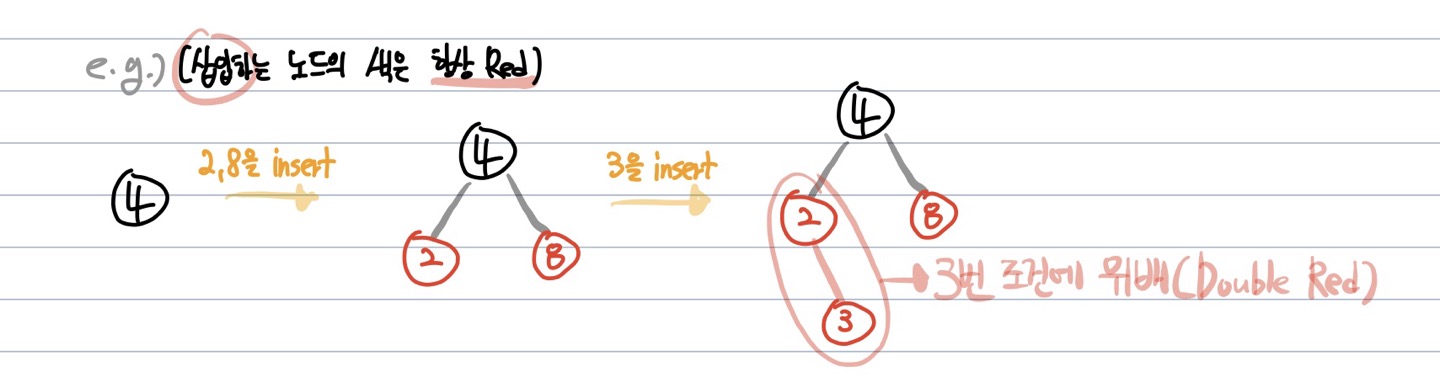
- 현재 insert된 node의 uncle node(부모노드의 형제 노드) 의 색깔에 따라 전략이 달라짐
1. uncle node가 Black인 경우 ➡️ Restructuring
- insert된 노드(z), parent node(v), uncle node(w)를 대상으로 Restructuring을 진행
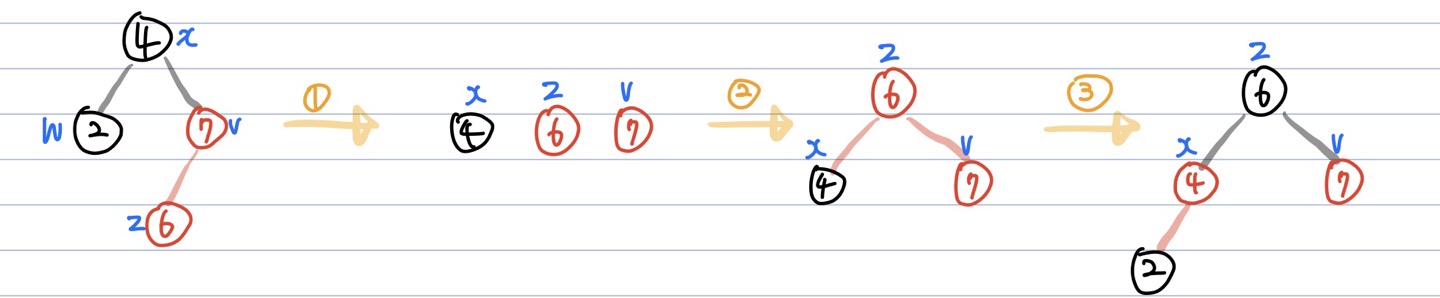
- 나, 부모, 부모의 부모를 오름차순으로 정렬
- 무조건 가운데 있는 값을 부모로, 나머지 둘을 자식므로 만듦
- 올라간 가운데 있는 값을 검정(Black) 으로 두 자식은 빨강(Red)으로 만듦
- 다른 서브트리에 영향(Depth Property)를 주지 않기 때문에 한 번의 Restructuring으로 끝남
- 위 예시에서 w노드를 보면 알 수 있듯이, Double Red를 해결하기 전후의 Black노드의 개수는 동일하기 때문에 다른 서브트리의 Black Property에 영향을 끼치지 않는다.
- 한 번의 Restructuring으로 끝나므로 이 자체는 O(1)의 시간복잡도 하지만, Double Red는 한 노드가 insert된 뒤 발생하므로 총 수행시간은 O(log(n))
- 어떤 node가 insert될 자리를 찾아야 하므로 logN의 시간이 소요
2. uncle node가 Red인 경우 ➡️ Recoloring
- insert된 노드(z), parent node(v), uncle node(w), grand parent node(x)를 대상으로 Recoloring을 진행
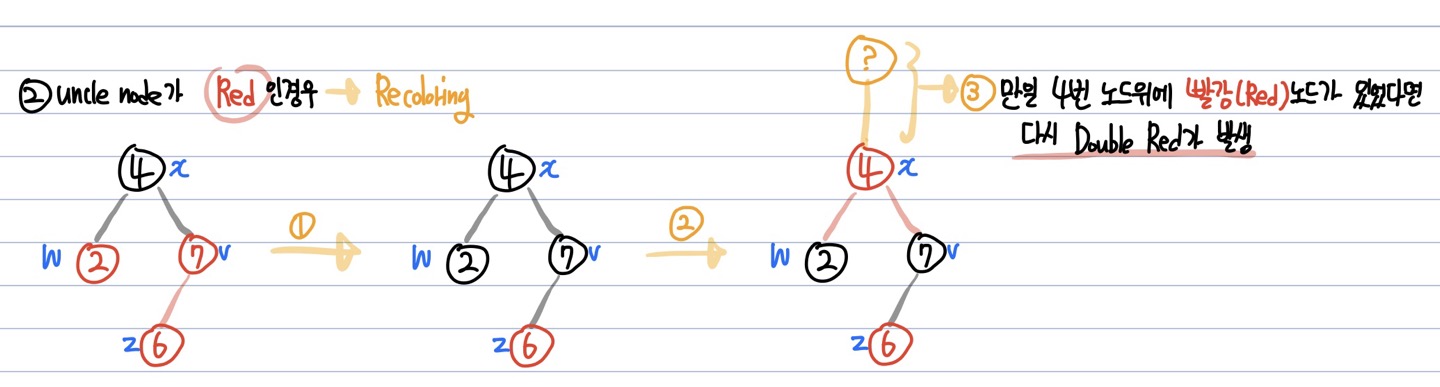
- 현재 insert된 노드(z)의 parent node(v)와 uncle node(w)를 검정(Black) 변경
- Grand Parent Node(x)를 빨강(Red)으로 변경
- Grand Parent Node가 Root Node가 아니라면(만일 Grand Parent위에 Red Node가 있었다면) 다시 Double Red가 발생할 수 있다.
- Black Depth는 일제히 1만큼 늘어나기 때문에 Depth Property를 만족
시간 복잡도
탐색 - O(logN)
삽입 - O(logN)
- Restructuring은 한 번만일어나므로 O(1), Recoloring은 다시 Double Red가 반복될 수 있으므로 최악의 경우 O(logN)
- 아무튼, 두 연사은 어떤 node를 insert한 뒤에 일어나고, insert 될 자리를 찾는데 최대 logN만큼 탐색한다.
- 따라서, Restructuring을 하든 Recoloring을 하든 총 수행시간은 O(logN)
Red Black Tree가 Balanced 한 이유
- 4번 조건(Depth Property)에 의해 Black Depth는 항상 같아야한다.
- 이때, root로부터 거리가 가장짧은 external node(1️⃣) 와 가장 긴 external node(2️⃣) 를 비교
- 1️⃣ : root부터 external node까지 거리가 가장 짧다 => Black Node만 존재하는 경우 (length = n)
- 2️⃣ : root부터 external node까지 거리가 가장 길다 => Black Node와 Red Node가 번갈아(검정->빨강->검정->빨강->...->검정) 존재하는 경우 (length = 2 * n)
- 1번 case와 2번 case의 길이는 2배차이. 따라서 Red-Black 트리의 서브트리간 높이 차이는 최대 2배이다
- Red-Black 트리의 높이는 항상 logN
AVL 트리 vs. Red-Black 트리
- AVL 트리
- 더욱 엄격한 균형(|BF| < 2), Red-Black 트리보다 더 빠른 조회를 제공
- 각 노드별로 BF를 저장해야하므로 노드마다 int(4byte) 자료형 만큼의 저장 공간이 필요
- 더 빠른 검색이 필요한 경우(데이터베이스 인덱싱, 파일시스템)에서 사용
- Red-Black 트리
- 상대적으로 느슨한 균형(두 서브트리의 높이 차이가 최대 2배)으로 인해 회전이 거의 이루어지지 않음
- AVL 트리보다 삽입/삭제가 용이
- 검정 혹은 빨강색만 표현하면 되므로 노드당 1비트만 필요(비트반전)
- 대부분의 언어 라이브러리(map, C++의 멀티캐스트, Java의 treeMap)에서 사용
참고한 곳
- https://zeddios.tistory.com/237
- https://velog.io/@agugu95/%EC%9D%B4%EC%A7%84-%ED%8A%B8%EB%A6%AC%EC%9D%98-%EA%B7%A0%ED%98%95-RED-BALCKAVL#red-black-vs-avl
반응형
'자료구조' 카테고리의 다른 글
| 세그먼트 트리(Segment Tree) (0) | 2021.12.24 |
|---|---|
| AVL 트리(AVL Tree) (0) | 2021.12.24 |
| B+ 트리(B+ Tree) (0) | 2021.12.24 |
| B 트리(B-Tree) (0) | 2021.12.24 |
| 트라이(Trie) (0) | 2021.12.24 |
Comments




